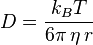In physics (namely, in kinetic theory) the Einstein relation is a previously unexpected connection revealed by Einstein in his 1905 paper on Brownian motion:
linking D, the Diffusion constant, and μ, the mobility of the particles; where kB is Boltzmann’s constant, and T is the absolute temperature.
The mobility μ is the ratio of the particle’s terminal drift velocity to an applied force, μ = vd / F.
This equation is an early example of a fluctuation-dissipation relation.
In the limit of low Reynolds number, the mobility μ is the inverse of the drag coefficient γ. For spherical particles of radius r, Stokes law gives
where η is the viscosity of the medium. Thus the Einstein relation becomes
This equation is also known as the Stokes-Einstein Relation. We can use this to estimate the Diffusion coefficient of a globular protein in aqueous solution: For a 100 kDalton protein, we obtain D ~10-10 m² s-1, assuming a “standard” protein density of ~1.2 103 kg m-3.
Also:
The word “viscosity” derives from the Latin word “viscum” for mistletoe. A viscous glue was made from mistletoe berries and used for lime-twigs to catch birds.
Isaac Newton postulated that, for straight, parallel and uniform flow, the shear stress, τ, between layers is proportional to the velocity gradient, ∂u/∂y, in the direction perpendicular to the layers, in other words, the relative motion of the layers.
 .
.
Here, the constant η is known as the coefficient of viscosity, the viscosity, or the dynamic viscosity. Many fluids, such as water and most gases, satisfy Newton’s criterion and are known as Newtonian fluids. Non-Newtonian fluids exhibit a more complicated relationship between shear stress and velocity gradient than simple linearity.
The relationship between the shear stress and the velocity gradient can also be obtained by considering two plates closely spaced apart at a distance y, and separated by a homogeneous substance. Assuming that the plates are very large, with a large area A, such that edge effects may be ignored, and that the lower plate is fixed, let a force F be applied to the upper plate. If this force causes the substance between the plates to undergo shear flow (as opposed to just shearing elastically until the shear stress in the substance balances the applied force), the substance is called a fluid. The applied force is proportional to the area and velocity of the plate and inversely proportional to the distance between the plates. Combining these three relations results in the equation F = η(Au/y), where η is the proportionality factor called the absolute viscosity (with units Pa·s = kg/(m·s) or slugs/(ft·s)). The absolute viscosity is also known as the dynamic viscosity, and is often shortened to simply viscosity. The equation can be expressed in terms of shear stress; τ = F/A = η(u/y). The rate of shear deformation is u / y and can be also written as a shear velocity, du/dy. Hence, through this method, the relation between the shear stress and the velocity gradient can be obtained.
In many situations, we are concerned with the ratio of the viscous force to the inertial force, the latter characterised by the fluid density ρ. This ratio is characterised by the kinematic viscosity, defined as follows:
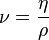 .
.
James Clerk Maxwell called viscosity fugitive elasticity because of the analogy that elastic deformation opposes shear stress in solids, while in viscous fluids, shear stress is opposed by rate of deformation.
Viscosity (dynamic/absolute viscosity): η or μ
The IUPAC symbol for viscosity is the Greek symbol eta (η), and dynamic viscosity is also commonly referred to using the Greek symbol mu (μ). The SI physical unit of dynamic viscosity is the pascal–second (Pa·s), which is identical to 1 kg·m−1·s−1. If a fluid with a viscosity of one Pa·s is placed between two plates, and one plate is pushed sideways with a shear stress of one pascal, it moves a distance equal to the thickness of the layer between the plates in one second. The name poiseuille (Pl) was proposed for this unit (after Jean Louis Marie Poiseuille who formulated Poiseuille’s law of viscous flow), but not accepted internationally. Care must be taken in not confusing the poiseuille with the poise named after the same person!
The cgs physical unit for dynamic viscosity is the poise[1] (P; IPA: [pwaz])) named after Jean Louis Marie Poiseuille. It is more commonly expressed, particularly in ASTM standards, as centipoise (cP). The centipoise is commonly used because water has a viscosity of 1.0020 cP (at 20 °C; the closeness to one is a convenient coincidence).
- 1 P = 1 g·cm−1·s−1
The relation between Poise and Pascal-second is:
- 10 P = 1 kg·m−1·s−1 = 1 Pa·s
- 1 cP = 0.001 Pa·s = 1 mPa·s
Kinematic viscosity: ν
Kinematic viscosity (Greek symbol: ν) has SI units (m2·s−1). The cgs physical unit for kinematic viscosity is the stokes (abbreviated S or St), named after George Gabriel Stokes. It is sometimes expressed in terms of centistokes (cS or cSt). In U.S. usage, stoke is sometimes used as the singular form.
- 1 stokes = 100 centistokes = 1 cm2·s−1 = 0.0001 m2·s−1.
- 1 centistokes = 1 mm²/s
Dynamic versus kinematic viscosity
Conversion between kinematic and dynamic viscosity, is given by νρ = η. Note that the parameters must be given in SI units not in P, cP or St.
For example, if ν = 1 St (=0.0001 m2·s-1) and ρ = 1000 kg m-3 then η = νρ = 0.1 kg·m−1·s−1 = 0.1 Pa·s